课    题

相似三角形的判定3

初备人

李艳霞

审核人

九年级数学组

复备人

教学目标

1、掌握相似三角形的判定定理3，了解相似三角形判定定理的证明。

2、通过相似三角形的判定定理的探索以及相似三角形判定定理的证明过程，进一步感受几何研究的方法，

体会几何证明的威力，发展合情推理和演绎推理的能力。

重点难点

重点：掌握相似三角形的判定定理3

难点：灵活运用判定定理3解决问题

课前准备

(教具、预

习作业等)

学案、投影机

课堂教学内容设计

复备内容

一、课前延伸，预习反馈：

1.什么叫相似三角形?

2.到目前，你学了几种判定两三角形相似的方法呢?

类似于判定三角形全等的SSS方法，我们能不能通过三边间的关系来判定两个三角形相似呢？

二、答疑解惑，孕育新知：

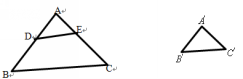
三、精讲精练，巩固新知

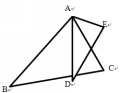
四、盘点知识，体验收获

相似三角形的判定定理3：三边成比例的两个三角形相似

五、达标检测，明确不足

1、一个三角形的三边长分别为8 cm,6 cm,12 cm,另一个与它相似的三角形的最短边为3 cm，则其余两边长为______________.

2、练一练: 已知△ABC和 △DEF,根据下列条件判断它们是否相似.

(1)  AB=3，    BC=4，    AC＝6

    DE＝6，  EF＝8，   DF＝9

(2)  AB=4，    BC=8，    AC＝10

    DE＝20，  EF＝16，   DF＝8

(3)  AB=12，    BC=15，    AC＝24

    DE ＝16，  EF＝20，   DF＝30

3、如图，某地四个乡镇A,B,C,D之间建有公路，已知AB=14千米，AD=28千米，BD=21千米， BC=42千米,DC=31.5千米，公路AB与CD平行吗？说出你的理由。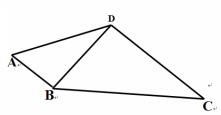

4、如图，在大小为4×4的正方形网格中，是相似三角形的是（     ）

①             ②            ③              ④

A．①和②       B．①和③       C．②和③       D．②和④

六、拓展提升，升华知识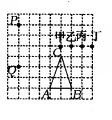

1、如图，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△PQR∽△ABC，则点R应是甲、乙、丙、丁四点中的（     ）        A．甲     B．乙  C．丙      D．丁

2、已知:如图,ΔABC中,∠ABC=2∠C,BD平分∠ABC.                      

求证:­AB·BC=AC­·CD.

七、布置作业，深化理解

八、本节示范课：

教学反思：